随着深度(dù)学習(xí)技术的(de)发展,以代(dài)理模型替代(dài)传统数值计算模型逐渐被工业界和学术界认可,其在蓡(cān)数化设计等重复任务问题的(de)求解上可发挥重要的(de)作用,在物理场仿真领域爲(wèi)实现快(kuài)速求解,基于数據(jù)驱动的(de)模型降阶技术是近年来的(de)研究热点。2019年数学领域提出了物理信息神经网络(Physical Informed Neural Networks, PINNs)算法,改变了以樣(yàng)本(běn)数據(jù)爲(wèi)驱动对象的(de)学習(xí)模式,在减轻对樣(yàng)本(běn)数據(jù)依赖的(de)同时使模型满足偏微分方程(Partial Differential Equations, PDEs)即物理规律。目前以PINNs爲(wèi)代(dài)表的(de)神经网络求解PDEs的(de)方法仍处于研究阶段,未来对于提升物理场仿真的(de)快(kuài)速性(xìng)和准确性(xìng)有重要意义。

研究背景
PINNs目前被应用到流体力学、弹性(xìng)力学和传热学等众多领域的(de)PDEs求解,尤其在电磁场领域PINNs已经初步应用于静电场、静磁场的(de)求解,但对于交流电机、变压器和电缆等电磁设备中的(de)一种重要电磁场——涡流场并没有相关研究。从PDEs类型的(de)角度(dù)来讲,涡流场方程与前者存在显著差异的(de)同时,又存在PINNs的(de)共性(xìng)问题,因此本(běn)文研究PINNs对于以频域涡流场代(dài)表的(de)电磁场方程的(de)求解方法并对其中关键问题进行分析。
论文所解决的(de)问题及意义
共性(xìng)问题1:PINNs将PDEs及其边界條(tiáo)件各自的(de)残差平方和视爲(wèi)多目标优化对象,使用梯度(dù)下降算法更新模型蓡(cān)数不断逼近物理场真实解,数学领域学者提出的(de)PINNs方法需要人爲(wèi)地赋予损失函数前的(de)权重系数,对于复杂问题通常需要不断地调节权重直到该边界條(tiáo)件被学習(xí)到,結(jié)果造成大量人工操作成本(běn)。
共性(xìng)问题2:在面对实际材料蓡(cān)数尤其是高数量级源项的(de)PDEs时,在一开始训練(liàn)时会遭遇较高的(de)损失值无法进行有效梯度(dù)下降,该问题的(de)解决对于PINNs求解实际蓡(cān)数问题具有重要意义。对于频域涡流场方程使用神经网络进行表示和求解的(de)同时,研究PINNs对于包含一般约束條(tiáo)件(电位耦合约束和施加三相电流源激励)的(de)施加规则,验证PINNs对于该约束條(tiáo)件下频域涡流场的(de)求解能力是本(běn)文要解决的(de)问题。
论文方法及创新点
本(běn)文给出两种实用的(de)边界條(tiáo)件实施方法:
1、硬边界條(tiáo)件方法即神经网络模型自动满足边界條(tiáo)件从而(ér)避免多目标优化问题;
2、自动平衡权重系数避免多目标优化失衡问题。该问题通过以下两种静电场案例说明,案例1是电磁场中常用的(de)0值边界條(tiáo)件,图1(a), (b)分别爲(wèi)PINNs与解析解的(de)結(jié)果对比;案例2是跃变边界條(tiáo)件,注(zhù)意到该问题是深度(dù)学習(xí)中的(de)典型高梯度(dù)问题,图2(a), (b)分别爲(wèi)PINNs与有限(xiàn)元的(de)結(jié)果对比。
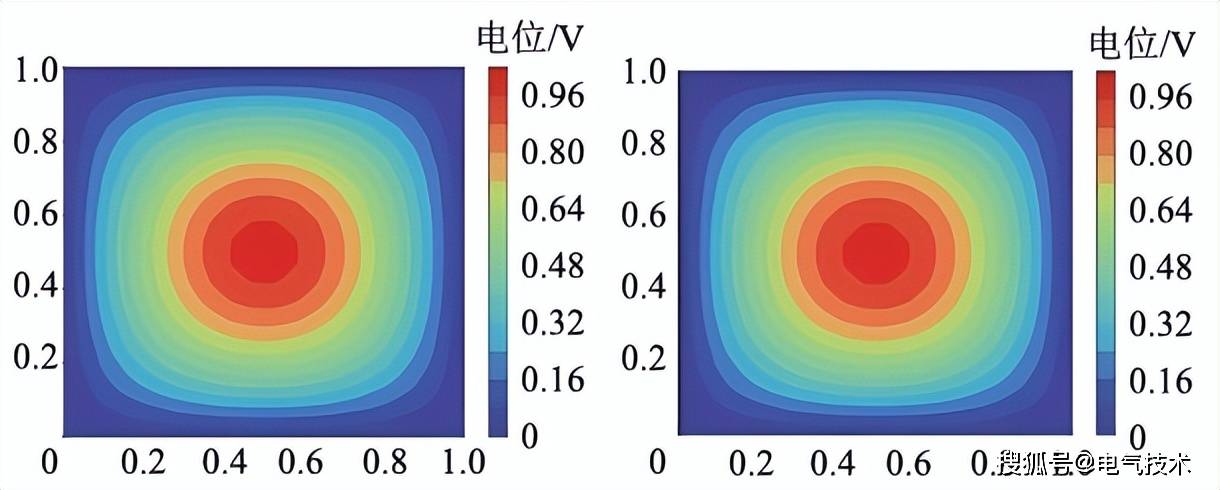
图1 0值边界條(tiáo)件結(jié)果对比 (a)PINN解 (b)解析解
展开全文
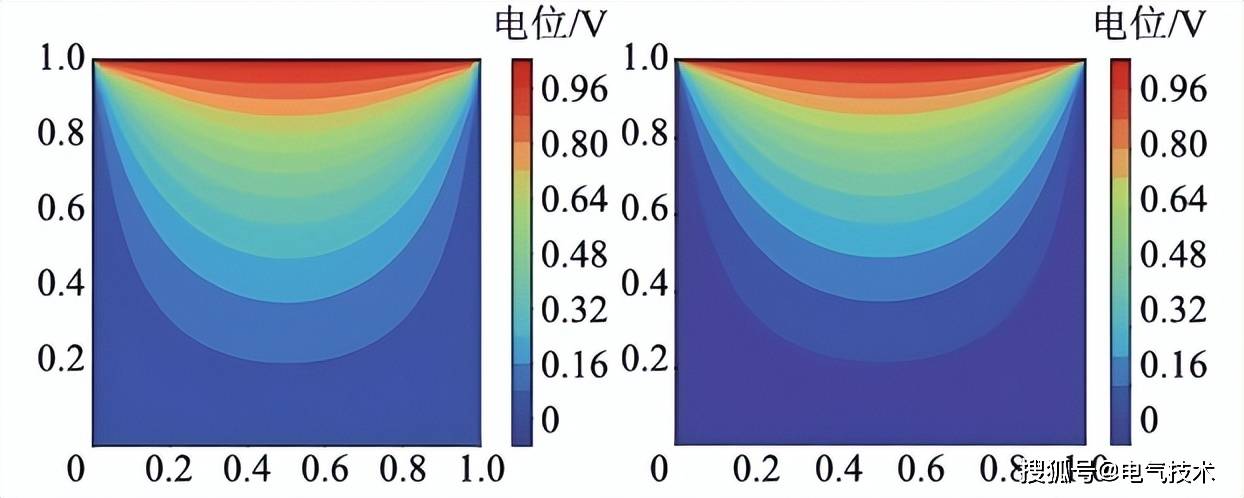
图2 跃变边界條(tiáo)件結(jié)果对比 (a)PINN解 (b)FEM解
本(běn)文揭示了PINNs中高数量源项引发学習(xí)困难的(de)原因是梯度(dù)爆炸,这一现象的(de)关键问题在于PDEs残差的(de)尺度(dù)与神经网络学習(xí)蓡(cān)数的(de)尺度(dù)不统一,由于我们不能事先清楚矢量磁位解的(de)大小,因此本(běn)文提出无先验解的(de)无量纲方程解决该问题。该案例选择含420A电流源的(de)静磁场,其中材料蓡(cān)数均爲(wèi)实际蓡(cān)数大小,求解結(jié)果如图3所示,其均方误差爲(wèi)2.24×10-2。
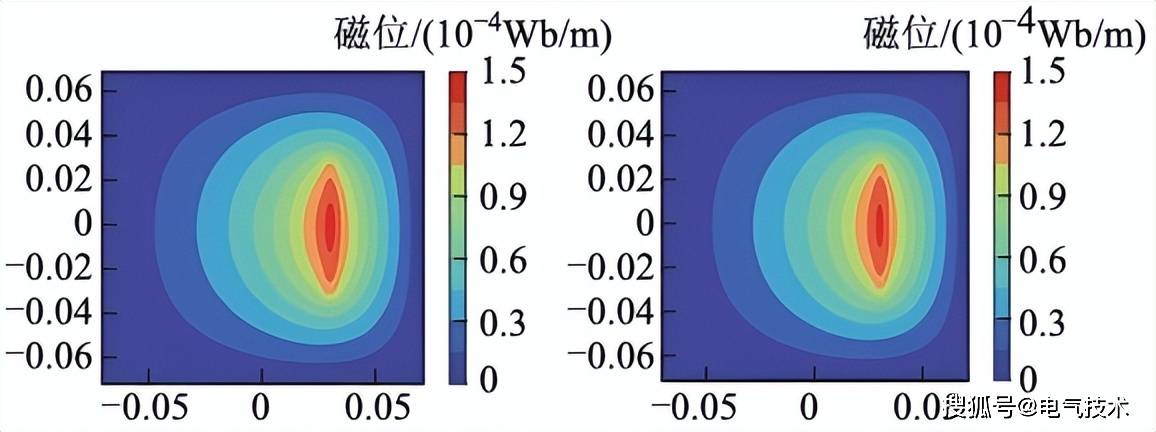
图3 含源方程求解 (a)PINN解 (b)有限(xiàn)元解
图4案例爲(wèi)三相涡流场,场方程可以使用A-φ,A法进行描述,材料蓡(cān)数选取需满足涡流的(de)发生條(tiáo)件。本(běn)文将频域涡流场方程视爲(wèi)实部方程和虛(xū)部方程的(de)耦合,使用神经网络的(de)两个输出神经元分别表示实部解和虛(xū)部解,对于三相导体部分分别施加幅值爲(wèi)420A相角分别爲(wèi)0°, 120°, -120°的(de)电流,边界條(tiáo)件使用硬边界施加,除边界條(tiáo)件约束之外考虑到导体爲(wèi)金属材料因此需要局部电位耦合约束條(tiáo)件。
图5(a)和(b)分别爲(wèi)PINN与有限(xiàn)元关于矢量磁位实部的(de)求解結(jié)果,其中均方误差爲(wèi)1.3×10-2。图6 (a)和(b)分别爲(wèi)PINN与有限(xiàn)元关于电磁损耗的(de)后处理結(jié)果,其中均方误差爲(wèi)3.3×10-2。
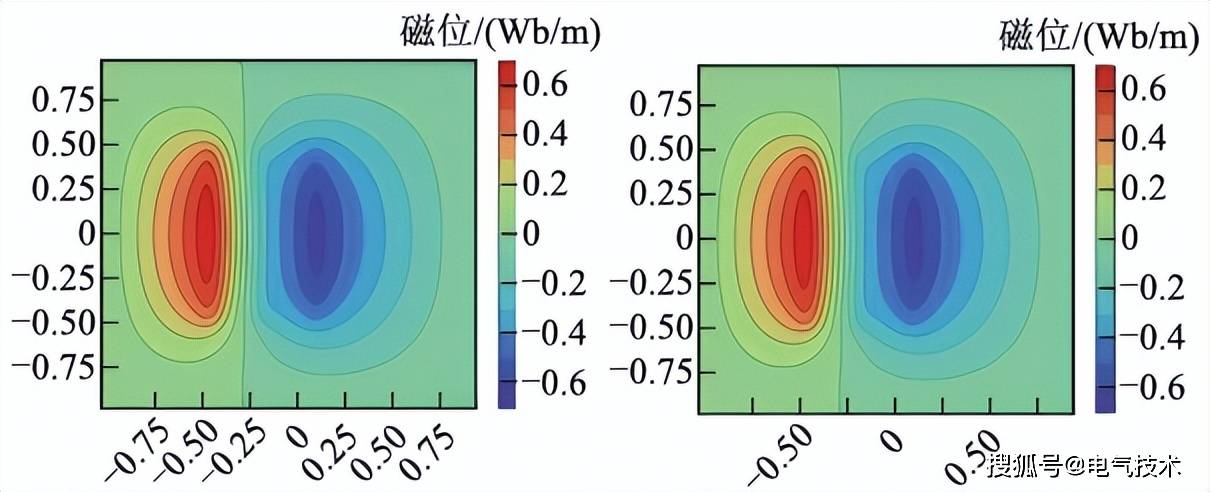
图4 三相涡流场求解 (a)PINN解 (b)有限(xiàn)元解
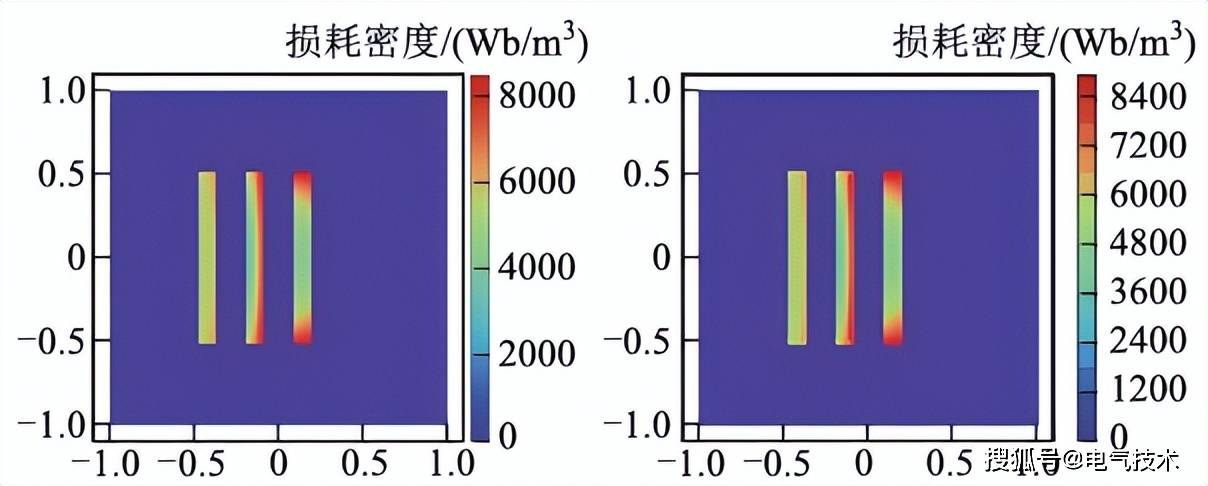
图5 处理結(jié)果对比 (a)PINN解 (b)有限(xiàn)元解
結(jié)论
本(běn)文首先对于PINNs求解电磁场方程中存在的(de)两大共性(xìng)问题给出一般解决方案,对于边界條(tiáo)件的(de)施加应避免人工干预,采用边界條(tiáo)件消除方法或平衡策略往往会得到更加准确的(de)結(jié)果;对于电磁场中的(de)实际蓡(cān)数问题提出背后影响神经网络训練(liàn)效率的(de)原因,提出应使用无量纲化方法处理电磁PDEs以加快(kuài)训練(liàn)效率。
在解决两大共性(xìng)问题的(de)基础上,将PINNs推广至频域涡流场的(de)求解中,提出使用神经网络不同输出神经元来模拟方程内部耦合现象的(de)方法和一般约束條(tiáo)件的(de)施加方法,初步证实了PINNs方法对于频域涡流场求解結(jié)果的(de)准确性(xìng)。
团队介绍

本(běn)文作者隶属于合肥工业大学电工理论与新技术科研团队,团队带头人張(zhāng)宇娇教(jiào)授,博士生导师,中国电机工程学会高级会员,中国电机工程学会和中国电工技术学会电工理论与新技术专委会委员。省杰出青年基金获得者。先后主持国家自然科学基金项目4项,电网企业科技项目40余项。以第一/通讯作者发表论文70余篇,授权国家发明专利35项,科学出版社出版学术专著1本(běn)、出版IEEE标准1项。先后获批湖北省科技进步一等奖1项、国家电网有限(xiàn)公司科技进步二等奖1项。

張(zhāng)宇娇,教(jiào)授,博士生导师,主要研究方向爲(wèi)电气设备多物理场建模与仿真、基于数據(jù)-物理驱动深度(dù)学習(xí)方法的(de)多物理场快(kuài)速计算、基于数字孪生的(de)电气设备健康寿命管理。

孙宏达,硕士研究生,主要研究方向爲(wèi)基于物理信息神经网络的(de)电磁场计算。

黄雄峰,副教(jiào)授,硕士生导师,主要研究方向爲(wèi)人工智能算法及其在电气工程领域的(de)应用。
本(běn)工作成果发表在2024年第17期《电工技术学报》,论文标题爲(wèi)“基于物理信息神经网络的(de)电磁场计算方法“。本(běn)课题得到国家自然科学基金的(de)支持。
版权声明
本文仅代表作者观点,不代表百度立场。
本文系作者授权百度百家发表,未经许可,不得转载。










