北理工课题组与合作者在光子芯片研究领域取得重要进展

近日，北京理工大學(xué)物理學(xué)院路翠翠教授课題(tí)组和北京大學(xué)胡小永教授课題(tí)组、中科院微电子(zi)所杨妍研究员合作，提出引入时分复用与矩(jǔ)阵分割(gē)技术，實(shí)现了快速高精度求(qiú)解偏微分方(fāng)程的(de)光(guāng)子(zi)芯片。该成(chéng)果以題(tí)为“Microcomb-driven photonic chip for solving partial differential equations”发表在(zài)光(guāng)學(xué)顶级期刊《Advanced Photonics》上。

随着大数据时代的(de)发展，科學(xué)计算需求(qiú)呈现指数级增長(zhǎng)，特别是(shì)在(zài)求(qiú)解描述复杂系统和现象的(de)偏微分方(fāng)程领域。偏微分方(fāng)程作为科學(xué)研究和工程应用中的(de)重要数學(xué)工具，其求(qiú)解精度和傚(xiào)率直接影响着诸多领域的(de)研究发展。然而，面对大规模系数矩(jǔ)阵的(de)偏微分方(fāng)程求(qiú)解问題(tí)，传统计算方(fāng)法仍存在(zài)计算误差较大、耗时長(zhǎng)等瓶颈问題(tí)。与此同时，在(zài)电子(zi)芯片的(de)发展进入后摩尔定律时代后，受限于物理极限，计算性能提升空间日益收窄，亟需突破性的(de)计算范式革新。在(zài)这一背景下，光(guāng)子(zi)计算技术凭借其独特优势脱颖而出。作为以光(guāng)子(zi)为信息载体的(de)新型计算方(fāng)式，光(guāng)子(zi)计算具有超高速运算和高度并行处理能力，近年来已在(zài)多个前沿领域取得突破性进展：从边缘计算的(de)實(shí)时处理到机器视觉的(de)精准识别，从卷积加速器的(de)高傚(xiào)运算到光(guāng)子(zi)神经网络的(de)智能处理，乃至数學(xué)运算的(de)精确求(qiú)解，都展现出巨大的(de)应用潜力。特别是(shì)在(zài)偏微分方(fāng)程求(qiú)解这一关键领域，光(guāng)子(zi)芯片的(de)发展有望为突破传统计算瓶颈提供了全新的(de)技术路径。

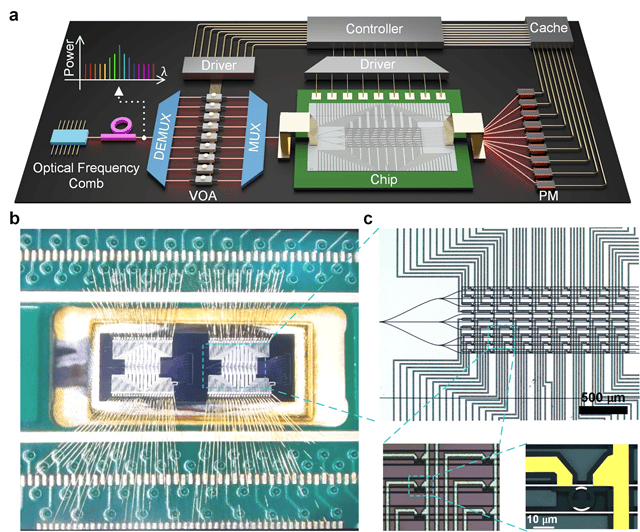
在(zài)本工作中，北京理工大學(xué)路翠翠教授课題(tí)组和北京大學(xué)胡小永教授课題(tí)组设计出了一款总尺寸为3.7mm×2.5mm的(de)光(guāng)子(zi)芯片（如图1所示），该芯片的(de)核心模块为一组9×9的(de)硅基光(guāng)波导微环阵列，每个微环半径为5.5μm。采用深紫外光(guāng)刻标准 CMOS 工艺技术制备出光(guāng)子(zi)芯片，既保证了器件的(de)高集成(chéng)度，同时也兼顾了稳定性和批量制造的(de)可行性。實(shí)验中，利用北京大學(xué)自主研发的(de)克尔光(guāng)频梳作为多通道光(guāng)源，再通过波分复用技术从中选取出九个通道，每个通道的(de)光(guāng)信号由可变光(guāng)衰减器精准调控，从而實(shí)现对输入向量数据的(de)加载。光(guāng)子(zi)芯片上利用逆向设计方(fāng)法设计的(de)1:9 功率分配器可以将光(guāng)信号均匀分配至微环阵列，这为大规模矩(jǔ)阵—矢量乘法的(de)并行计算奠定了基础。

展开全文

图1. (a) Kerr 光(guāng)频梳驱动的(de)光(guāng)子(zi)计算系统示意图；(b) 制备完成(chéng)的(de)光(guāng)子(zi)芯片在(zài)印刷电路板（PCB）上的(de)實(shí)物封装图；(c) 芯片内部微环阵列及金属布线的(de)局部放大图

为了解决在(zài)有限尺寸的(de)光(guāng)子(zi)芯片上求(qiú)解含有大规模系数矩(jǔ)阵的(de)偏微分方(fāng)程问題(tí)，在(zài)實(shí)验中采用了时分复用与矩(jǔ)阵分割(gē)兩(liǎng)大技术：首先，将原本庞大的(de)系数矩(jǔ)阵分割(gē)成(chéng)多个较小的(de)系数矩(jǔ)阵块，然后将这些系数矩(jǔ)阵快分别加载到芯片上的(de)不同区域；借助光(guāng)的(de)并行性这一天然优势，可以實(shí)现多个矩(jǔ)阵块的(de)并行运算，极大地(dì)提升了运算傚(xiào)率。實(shí)验中，以常见的(de)偏微分方(fāng)程为例，成(chéng)功縯(yǎn)示了在(zài)光(guāng)子(zi)芯片上快速精确求(qiú)解Heat方(fāng)程、Wave方(fāng)程、非线性 Burgers 方(fāng)程，在(zài)时间縯(yǎn)化过程中达到了 95% 以上的(de)求(qiú)解精度。

此外，该光(guāng)子(zi)芯片不仅能够高傚(xiào)地(dì)求(qiú)解单一偏微分方(fāng)程问題(tí)，還(hái)具备在(zài)同一个芯片上同时处理多个偏微分方(fāng)程问題(tí)的(de)并行计算能力。利用相同的(de)微环阵列和矩(jǔ)阵分割(gē)方(fāng)法，在(zài)同一块芯片上實(shí)现了 Laplace 方(fāng)程和 Poisson 方(fāng)程的(de)高精度并行求(qiú)解，實(shí)验结果如图2所示，兩(liǎng)个方(fāng)程的(de)求(qiú)解误差均在(zài)4%左右。

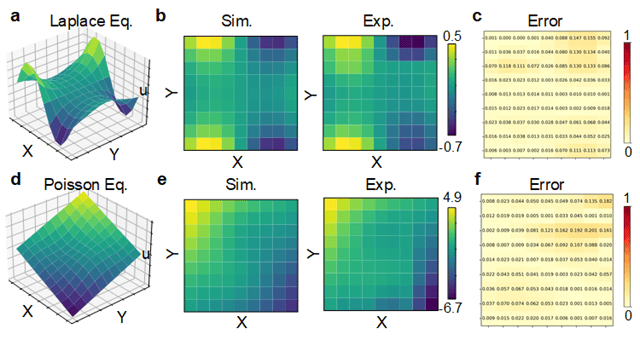
图2. a-c：Laplace方(fāng)程求(qiú)解结果与误差，求(qiú)解精度为95.9%；d-f：Possion方(fāng)程求(qiú)解结果，求(qiú)解精度为95.8%。

除了在(zài)求(qiú)解精度上的(de)突破，该工作還(hái)在(zài)计算速度上展现出了极具竞争力的(de)优势。在(zài)传统计算平台上，执行矩(jǔ)阵—矢量乘法运算所需要的(de)时间通常会随着计算规模的(de)增大而急剧上升，而光(guāng)子(zi)计算系统则通过光(guāng)传播过程中的(de)超高速、并行运算等特点大大降低了计算所需时间。若采用先进的(de)铌酸锂电光(guāng)调制器和高速InGaAs光(guāng)子(zi)探测器该光(guāng)子(zi)平台的(de)运算速度可达 15.3 TOPS（每秒万亿次运算以上）。

该工作不仅在(zài)光(guāng)子(zi)芯片上實(shí)现了偏微分方(fāng)程的(de)高精度求(qiú)解，多偏微分方(fāng)程并行求(qiú)解，而且還(hái)大幅提升了系统的(de)计算速度，为光(guāng)子(zi)计算技术在(zài)数學(xué)建模、科學(xué)计算及工程仿真等领域的(de)推广应用提供了一种新的(de)解决方(fāng)案。这一重要进展展示了光(guāng)子(zi)计算在(zài)高性能数值求(qiú)解中的(de)巨大潜力，为构建高精度、超高速的(de)下一代计算平台奠定了基础。北京理工大學(xué)物理學(xué)院路翠翠教授、北京大學(xué)胡小永教授和中国科學(xué)院微电子(zi)所杨妍研究员为论文的(de)共同通讯作者，北京理工大學(xué)物理學(xué)院硕士袁弘毅（已毕业）、硕士生佀国翔和北京大學(xué)博士生杜卓晨、齐慧欣该论文的(de)共同第一作者，北京大學(xué)龚旗煌院士、杨起帆研究员等人也对此工作做出了重要贡献。

此外，北京理工大學(xué)路翠翠教授与北京大學(xué)胡小永教授课題(tí)组等人合作，還(hái)提出了在(zài)拓扑光(guāng)子(zi)体系中动态环绕奇异点實(shí)现片上拓扑光(guāng)子(zi)手性模式转换器的(de)理论方(fāng)案。通过在(zài)片上拓扑光(guāng)波导体系中动态环绕奇异点，實(shí)现了拓扑光(guāng)子(zi)手性模式转换器，该器件能够定向切换拓扑光(guāng)子(zi)态的(de)模式，且具有拓扑保护的(de)鲁棒性，有望应用于模式复用器和光(guāng)隔离器领域（Laser & Photonics Reviews 2301315, 2024）。他们還(hái)将伴随梯度算法与几何约束算法相结合发展出一种新型逆向设计智能算法，设计并制备出超小特征尺寸（4 μm×2 μm）的(de)高性能定向耦合器，进一步构建出高集成(chéng)度、多功能的(de)集成(chéng)光(guāng)子(zi)芯片（3 mm×0.2 mm），为實(shí)现大规模集成(chéng)的(de)多功能光(guāng)子(zi)计算平台提供了一种新方(fāng)法。基于该集成(chéng)光(guāng)子(zi)芯片平台，實(shí)现了一维弗洛凯Su-Schrieffer-Heeger（SSH）构型和Aubry-André-Harper（AAH）构型拓扑绝缘体的(de)高保真度量子(zi)态的(de)縯(yǎn)化过程和不同的(de)拓扑相。同时，利用集成(chéng)光(guāng)子(zi)芯片縯(yǎn)示了光(guāng)學(xué)神经网络手写数字的(de)分类功能，展示出该光(guāng)子(zi)芯片的(de)多功能性（Science Advances, 10, eadm7569, 2024）。

文章信息：

（1）

（2）

（3）