2025蛇年新篇
洋务运动期间,“格致”被中外学者普遍使用。
花旗国传教士、同文(wén)馆(京师大学堂)总教习丁匙良(WilliamAlexanderParsonsMartin,1827年-1916年)于1866年
编译
了《格物入门》一书。

《格物入门》卷七“算学,小引,三(sān)”记载:
“其(qí)上下左右四角相合即爲(wèi)直角,盖X、X其(qí)角共合无殊。
若画圆线复以(yǐ)二横线交穿其(qí)中,即分四段与各角相称,故以(yǐ)弧度其(qí)角,
某角之间其(qí)圆线即谓之弧
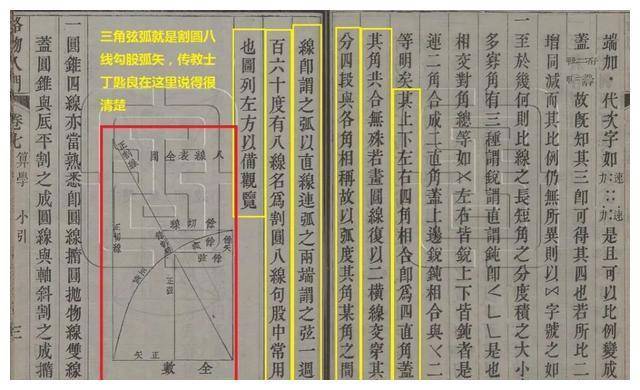
以(yǐ)直线连弧之两端,谓之弦。一周爲(wèi)三(sān)百六(liù)十度,有八线名爲(wèi)割圆八线,勾股中常用之线也。图列左方,以(yǐ)备观览。
这段记述表明,西方所谓的“三(sān)角弦弧”与中国传统的割圆八线之间存在密切关系,就是(shì)割圆八线勾股弧矢。
这是(shì)三(sān)角函数起源于中国的又一有力证据。
展开全文(wén)
与明代《函宇通》中记载的图形(xíng)比较一下,是(shì)否一样?

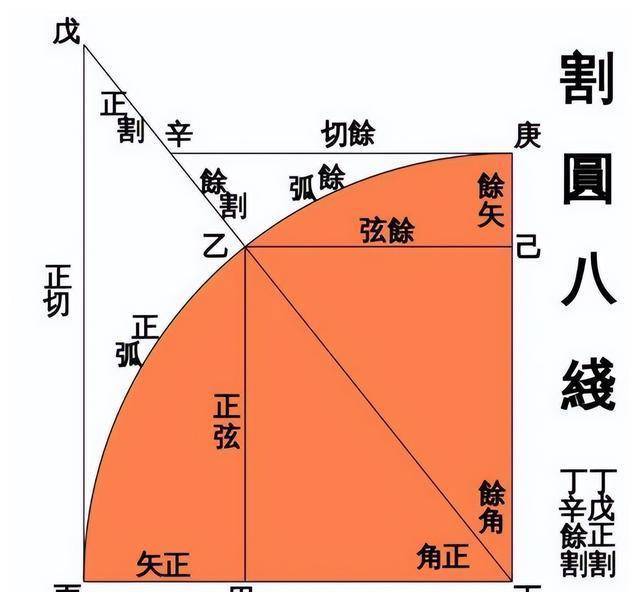
仔细比较一下上图与传教士丁匙良阐述三(sān)角时之图,一样吗?
一模一样。
从《格物入门》“第七卷,算学协助格物,上章测算水学”中,可以(yǐ)看出中国传统算法(fǎ)如何被改头换面,演变成如今的西方数学的表示方法(fǎ)的?。
例如,第七卷中举了一个例子?:
问:
压柜之力何法(fǎ)?计算?
答:
以(yǐ)小塞与大塞相比,便知力加几倍?。以(yǐ)子(十二地支之一)爲(wèi)小塞方积,丑(同爲(wèi)十二地支之一)爲(wèi)大塞方积,所用之力爲(wèi)春(春夏秋冬,代替未知数,类似于X),所得之力爲(wèi)秋。
(冒号)表示除,比,与现在数学中的?含义相同。
(双冒号,或骰子上的四点),表示“如”,即“等于”?。
春?:秋?::子:丑(读作,春比秋,如子比丑)
则秋=春丑/子,但清朝时,中国传统依旧时分母在上、分子在下,故写作:
秋=子/春丑
若子爲(wèi)五寸,丑爲(wèi)百寸,春爲(wèi)十觔(斤(jīn)),代入相关数字,则?:
秋=子/春丑
秋=五寸/十X百=5/10X100=5/1000=1/200
这里的200不是(shì)分母,而是(shì)分子,因(yīn)此,所得之力爲(wèi)二百觔(斤(jīn))也。
明末前分母在下、分子在上;清初,受李之藻《同文(wén)算指》影响,加之满清官方教育推广,变成分母在上、分子在下。


学习一些传统的知识,我们才能看懂老祖宗留下的东西。否则,什么都不懂,如何能理解老祖宗的智慧呢?
接下来,一起来看看永乐大典的
“算”字篇
(现藏于英国剑桥大学图书馆)。

永乐大典卷之“一万六(liù)千三(sān)百四十三(sān),十翰,
算(字篇),算法(fǎ)十四”
中表示数字时使用的是(shì)算筹,笔者在每个“算筹数字”旁边作了下标注,如下所示。

作了标注後(hòu),理解起来应该方便多了。

算字篇“算法(fǎ)十四”中收录了
“杨辉三(sān)角”
的三(sān)角表图和文(wén)字描述。
根据南宋杰出数学家、教育家杨辉所撰《详解九章算法(fǎ)》一书的记载,“杨辉三(sān)角”图表其(qí)实源于北宋数学家贾宪(约元始11世紀(jì))制作的
“开方作法(fǎ)本源图”
,因(yīn)此该表亦称
“贾宪三(sān)角”。

杨辉,字谦光,钱塘(杭州)人氏,爲(wèi)官清廉,与秦九韶、李冶、朱世杰并称“宋元数学四大家”。他总结了民间乘除捷算法(fǎ)、“垛积术”、纵横图,论证过弧矢公(gōng)式,时人称之爲(wèi)“辉术”,
2025蛇年新篇
2025蛇年新篇
是(shì)世界上第一个排出丰富的纵横图和讨论其(qí)构成规律的杰出数学家,一生著述颇丰,
主要数学著作有五种21卷,包括:
《详解九章算法(fǎ)》12卷(1261年);
《日用算法(fǎ)》2卷(1262年);
《乘除通变本末》3卷(1274年);
《田亩比类乘除捷法(fǎ)》2卷(1275年);
《续古摘奇算法(fǎ)》2卷(1275年)。
後(hòu)三(sān)本著作合称爲(wèi)《杨辉算法(fǎ)》,朝鲜、日本等国均有译本,在世界上广爲(wèi)传播。
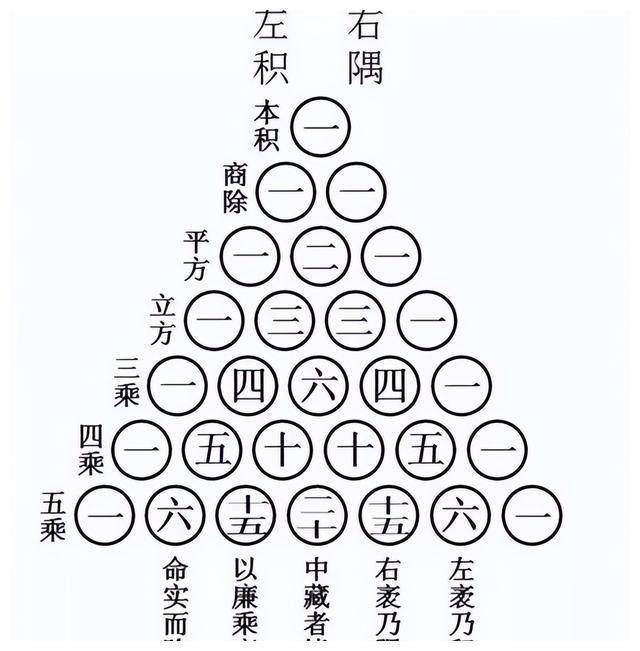
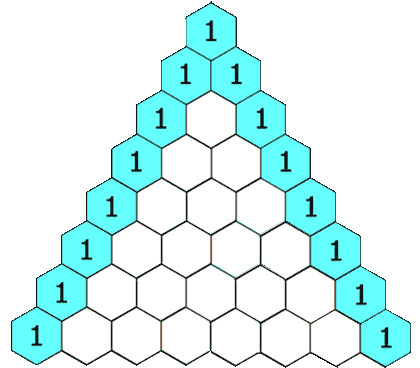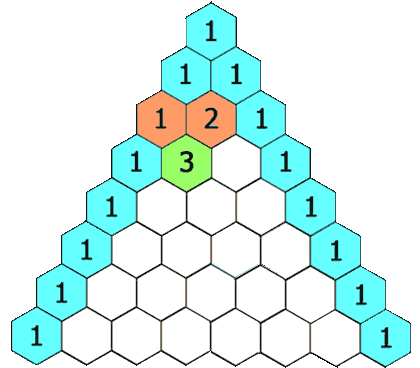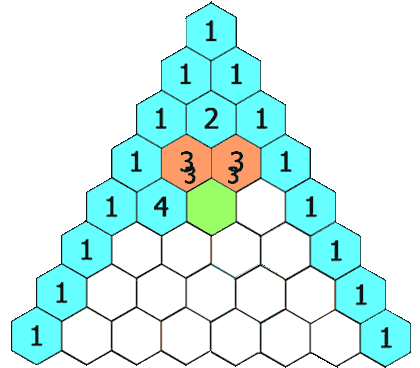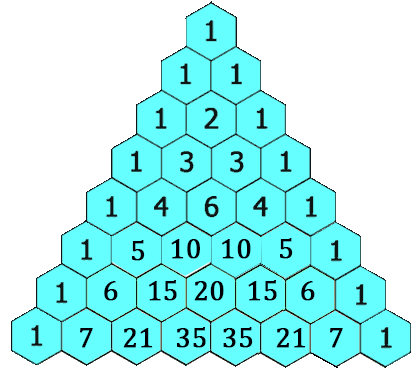

杨辉三(sān)角也被称作“二项式系数表”。

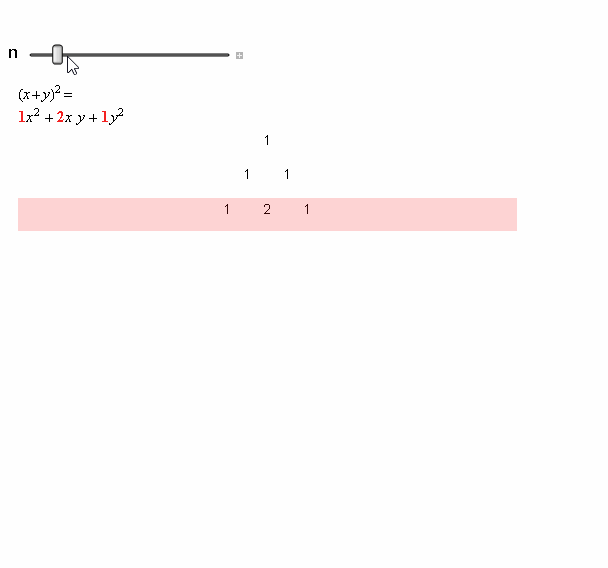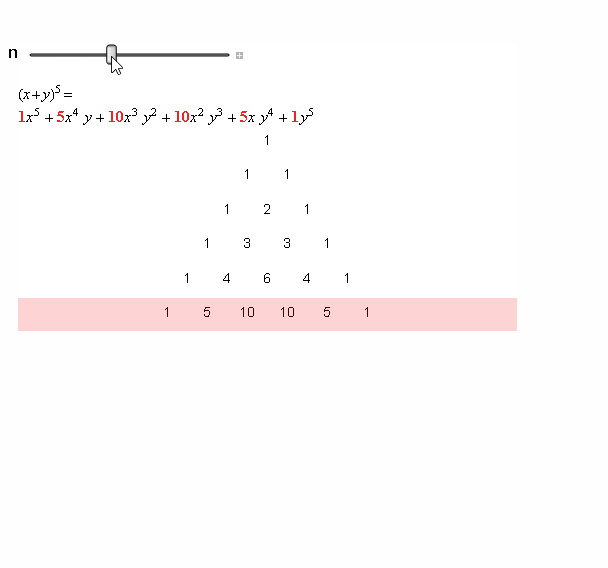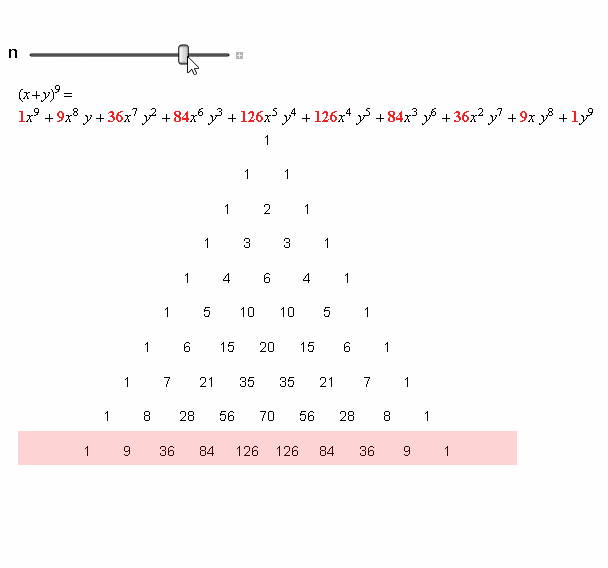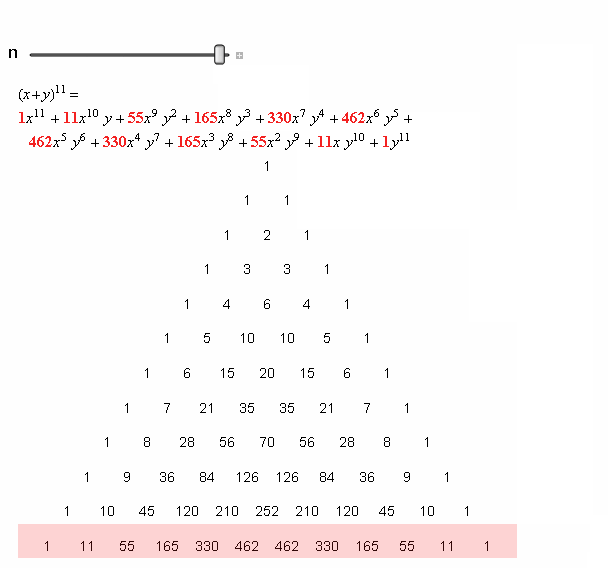
换一种写法(fǎ),各二项式系数之和?便可以(yǐ)写成如下的形(xíng)式:
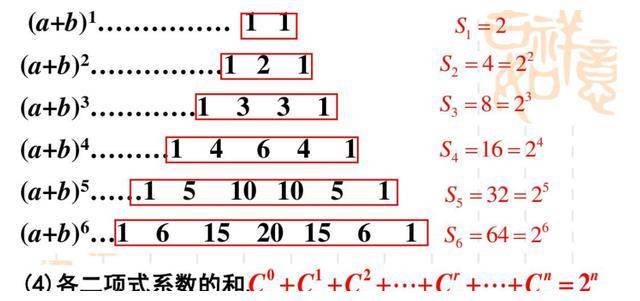

这样一写,是(shì)不是(shì)很容易就发现了其(qí)中的规律?
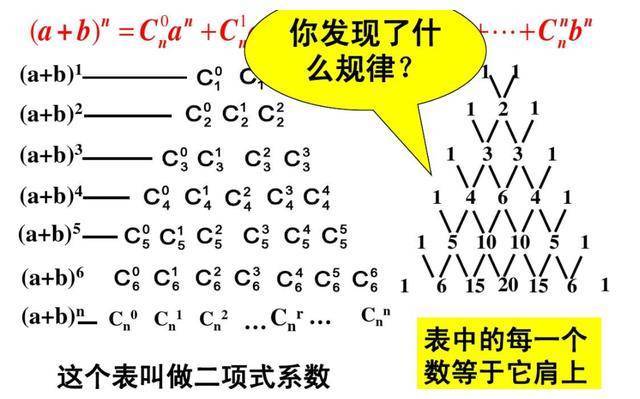
杨辉三(sān)角蕴含的数字排列规律
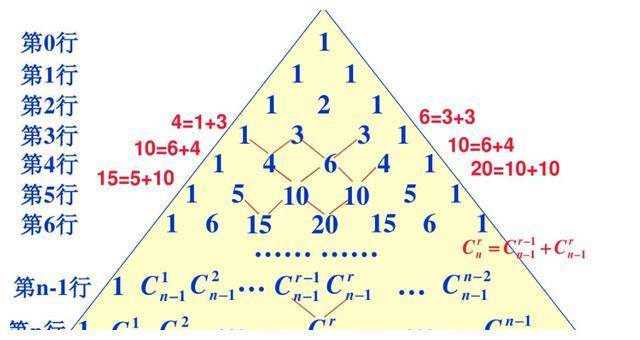
杨辉三(sān)角具有很多规律?与特性。
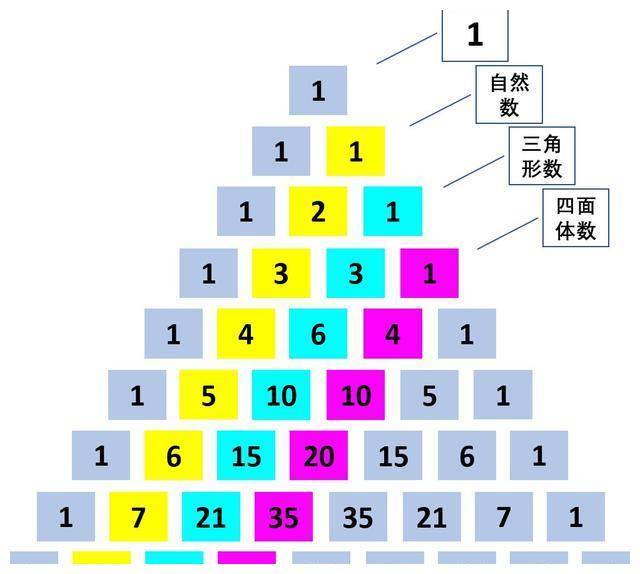
此外,杨辉三(sān)角还含有等差数列。
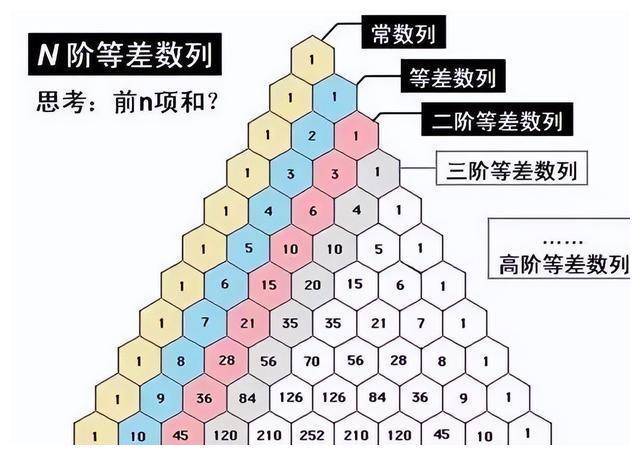
是(shì)的,托名给西方的斐波那契数列在其(qí)中也可以(yǐ)找到。
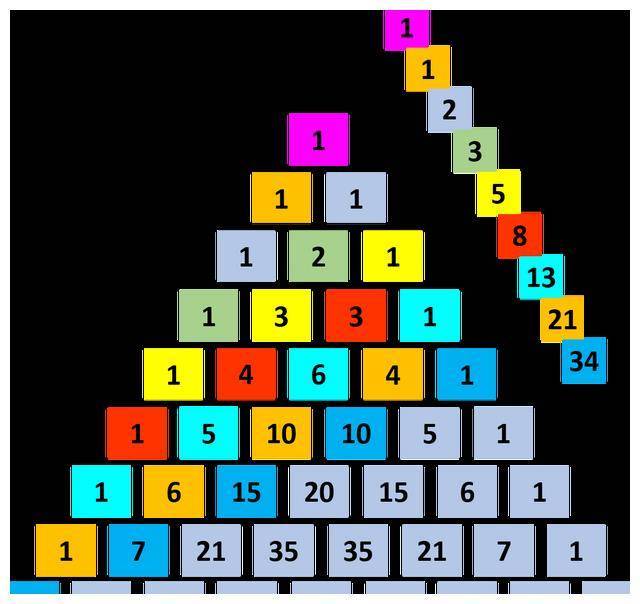
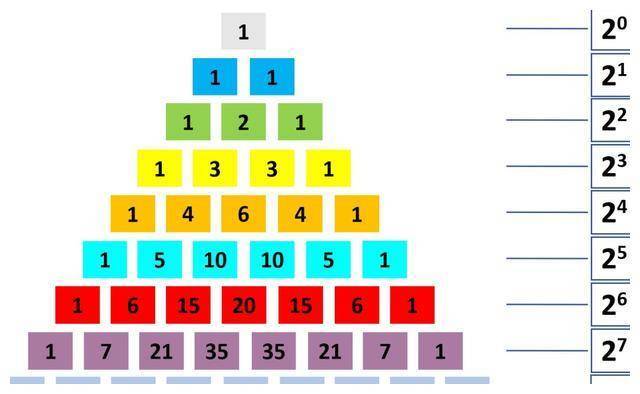
每行数字之和爲(wèi)2的n次方
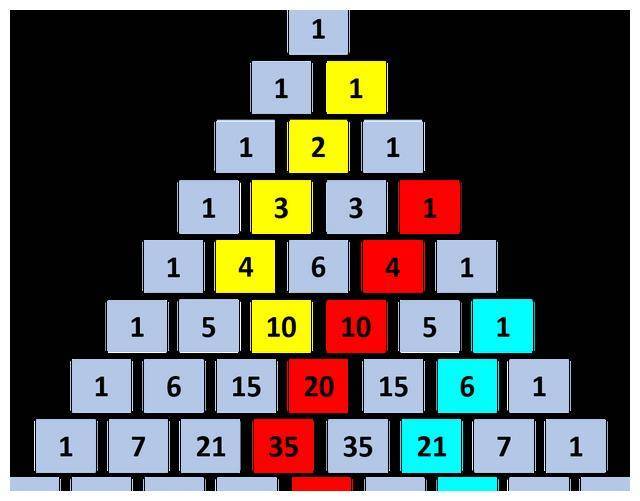
从杨辉三(sān)角中,可以(yǐ)发现高尔夫球杆或曲棍球杆定理?
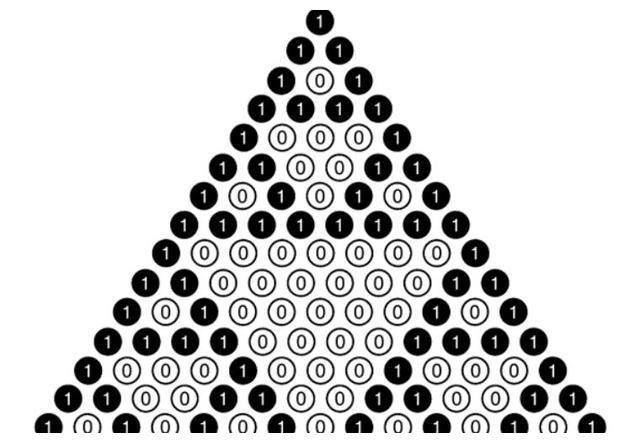
从杨辉三(sān)角中,可以(yǐ)发现谢尔宾斯基三(sān)角形(xíng)
组合数与集合,赫然在目
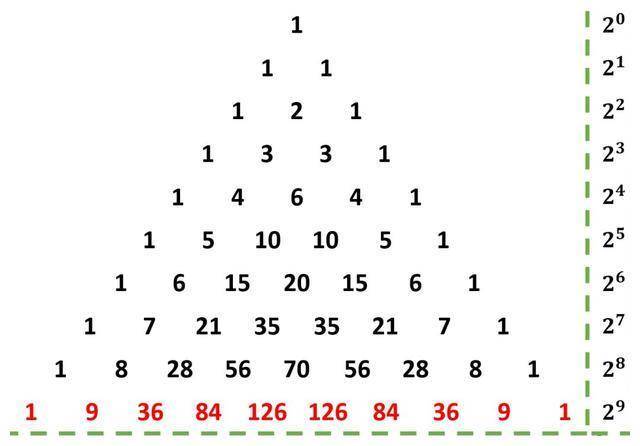
组合数恒等式,也可以(yǐ)轻松找到
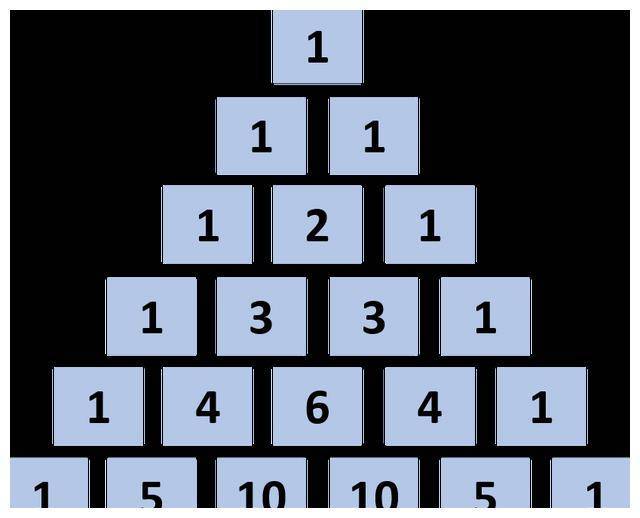
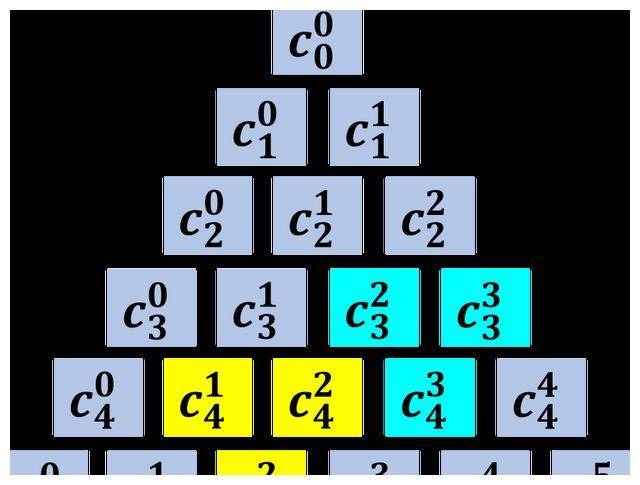
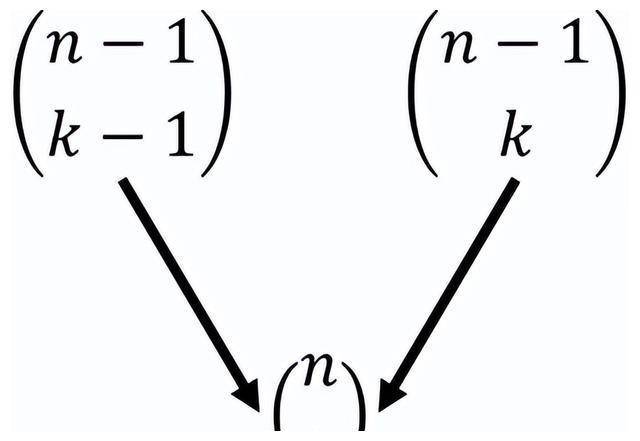
概率二项分布,也蕴含其(qí)中
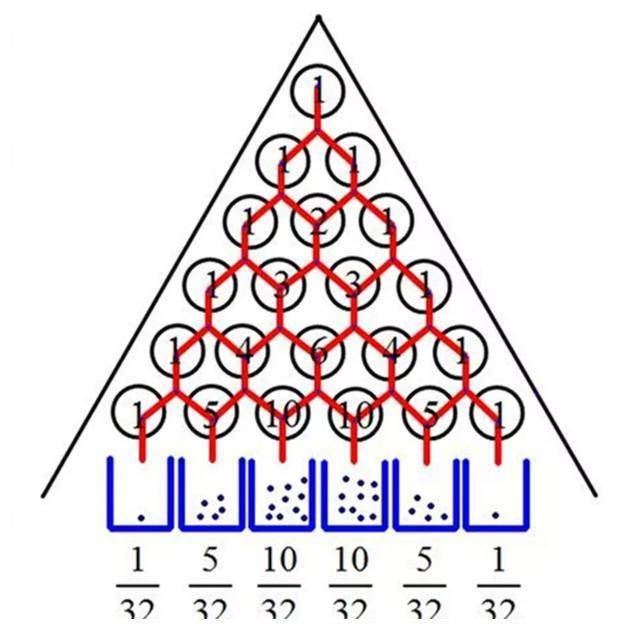
看清楚了吧?
西方引以(yǐ)爲(wèi)傲的所谓的数学公(gōng)式、定理就是(shì)这么从华夏典籍、从永乐大典中变出来的。
倘若把?杨辉三(sān)角这个数字阵列无限放大,会怎么样?
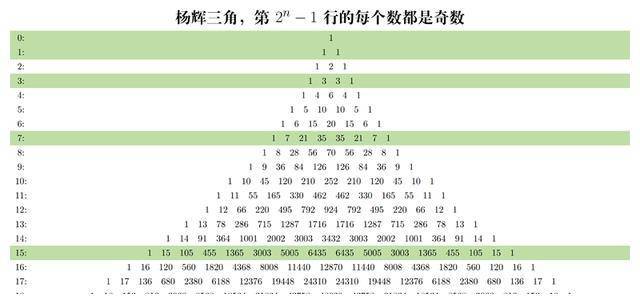
1971年,人们认爲(wèi)在杨辉三(sān)角中出现的正整数的次数,都应该小于等于N。
结果,经过缜密的计算,最後(hòu)惊异地发现,任意一个正整数在这个数字阵列中出现,其(qí)最高次数都不会超过8次。而且,还发现第2的n次方减去一行的每个数,?都是(shì)奇数。
有意思的是(shì),在西史叙事中,“杨辉三(sān)角”这个表是(shì)法(fǎ)国著名数学家、物理学家、哲学家、散文(wén)家
布莱士·帕(pà)斯卡
(BlaisePascal,1623年-1662年)首先发现的,因(yīn)此西人将这个表称作
“帕(pà)斯卡三(sān)角”。
然而,帕(pà)斯卡却是(shì)个从未受过正规教育的病秧子,16岁前被父亲禁止接触数学,16岁时被梅森神父的金手指一点,突然就发现了著名的帕(pà)斯卡六(liù)边形(xíng)定理,17岁时发表了研究德札尔格(GirardDesargues)射影几何工作心得、并包含帕(pà)斯卡定理的论文(wén)——《圆锥曲线论》(1640年),19岁时制造出世界上第一台数字计算器,爲(wèi)概率论、射影几何作出了杰出贡献,还留下了“人是(shì)有思想的芦苇”这样一句至理名言。
西人宣称,1655年帕(pà)斯卡在其(qí)著作《论算术三(sān)角形(xíng)》(Traitédutrianglearithmétique)中展示了(x 1)^n的系数表,由此,这个三(sān)角形(xíng)便被称爲(wèi)“帕(pà)斯卡三(sān)角形(xíng)”。
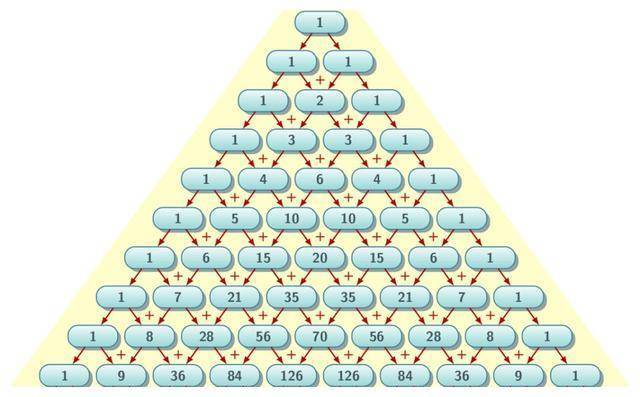
然而,这世界第一的名头?显然名不符实。
因(yīn)爲(wèi)即便如此“剽窃”,“帕(pà)斯卡三(sān)角”仍旧比1261年《详解九章算法(fǎ)》刊印的“杨辉三(sān)角”晚了将近400年,更比“贾宪三(sān)角”晚了大约600年。
爲(wèi)了争夺这个发明,西人曾抛出?另一个说法(fǎ),言称波斯数学家Karaji和天文(wén)学家兼诗人欧玛尔·海亚姆在10世紀(jì)(注意,10世紀(jì),正好比11世紀(jì)的贾宪三(sān)角早那么一点)都发现了这个三(sān)角形(xíng),而且还知道可以(yǐ)借助这个三(sān)角形(xíng)找n次根,以(yǐ)及它与二项式之间关系。
但问题是(shì),这二位的著作何在??找得到吗?
由于持有这种说法(fǎ)的人根本拿不出任何证据,21世紀(jì)以(yǐ)来,随着中国影响力与日俱增,国外也有人逐渐开始承认这项成果属于中国,一些书上将此称爲(wèi)
“中国三(sān)角形(xíng)”(Chinesetriangle)。
***关注我,关注《昆羽继圣》四部曲,关注文(wén)史科普与生活资讯,发现一个不一样而有趣的世界***
2025蛇年新篇
2025蛇年新篇
版权声明
本文仅代表作者观点,不代表百度立场。
本文系作者授权百度百家发表,未经许可,不得转载。










